이 연습에서는 로지스틱 회귀를 구현하여 두 가지 다른 데이터 세트에 적용합니다. 프로그래밍 연습을 시작하기 전에 비디오 강의를 시청하고 관련 주제에 대한 검토 질문을 완료하는 것이 좋습니다. 연습을 시작하려면 시작 코드를 다운로드하고 연습을 완료하려는 디렉토리에 해당 내용의 압축을 풀어야합니다. 필요한 경우이 연습을 시작하기 전에 Octave에서 cd 명령을 사용하여이 디렉토리로 변경하십시오. 코스 웹 사이트의 "Octave Installation"페이지에서 Octave를 설치하기위한 지침을 찾을 수도 있습니다.
ex2.m
- 운동을 통해 단계별로 도움이되는 옥타브 스크립트
ex2 reg.m - 연습의 뒷부분에 대한 옥타브 스크립트
ex2data1.txt - 연습의 첫 번째 절반을위한 교육 세트
ex2data2.txt - 연습의 후반을위한 교육 세트
submit.m - 솔루션을 Google 서버에 전송하는 제출 스크립트
mapFeature.m - 다항식 기능을 생성하는 함수
plotDecisionBounday.m - 분류 자의 결정 경계를 그릴 함수
[?] plotData.m - 2D 분류 데이터를 그리는 함수
[?] sigmoid.m - 시그 모이 드 함수
[?] costFunction.m - 로지스틱 회귀 비용 함수
[?] predict.m - 로지스틱 회귀 예측 함수
[?] costFunctionReg.m - 정규화 된 물류 회귀 비용
? 완료해야 할 파일을 나타냅니다.
연 습을 하면서 ex2.m 및 ex2 reg.m 스크립트를 사용하게 됩니다. 이 스크립트는 문제에 대한 데이터 세트를 설정하고 작성하는 함수를 호출합니다. 둘 중 하나를 수정할 필요가 없습니다. 이 과제의 지침에 따라 다른 파일의 함수 만 수정하면 됩니다.
이 부분에서는 학생이 대학에 입학 할 것인지를 예측하는 로지스틱 회귀 모델을 작성합니다.
귀 하가 대학 학부의 관리자이고 두 번의 시험에 대한 결과에 따라 각 신청자의 입학 확률을 결정한다고 가정하십시오. 이전 지원자의 과거 데이터를 사용하여 로지스틱 회귀에 대한 교육 세트로 사용할 수 있습니다. 각 교육 사례에 대해 두 가지 시험에 대한 지원자의 점수와 입학 결정이 있습니다.
귀 하의 임무는 두 시험의 점수에 따라 입학 가능성을 추정하는 분류 모델을 작성하는 것입니다. 이 개요 및 ex2.m의 프레임 워크 코드는 연습을 안내합니다.
학 습 알고리즘을 구현하기 전에 가능한 경우 데이터를 시각화하는 것이 좋습니다. ex2.m의 첫 번째 부분에서 코드는 데이터를로드하고 plotData 함수를 호출하여 2 차원 플롯에 표시합니다.
이 제 plotData에서 코드를 완료하여 그림 1과 같은 그림을 표시합니다. 여기에서 축은 두 개의 시험 점수이고 양수와 음수의 예제는 다른 표식과 함께 표시됩니다.
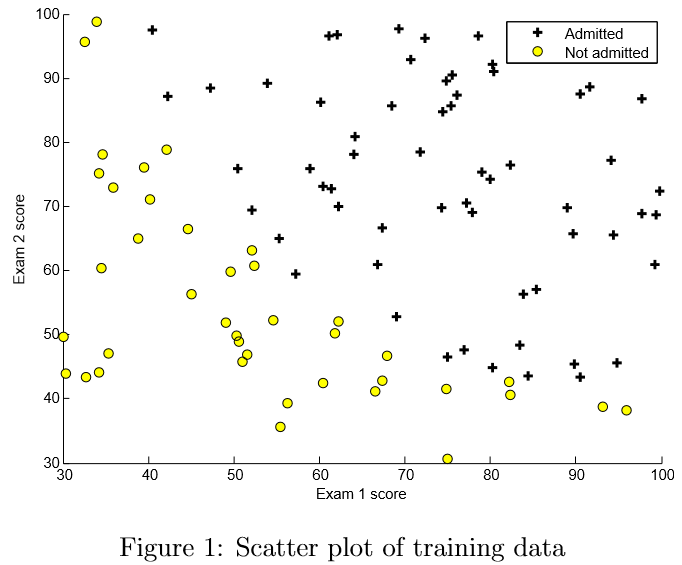
플 로팅에 더 익숙해 지도록 plotData.m을 비워 두어 직접 구현할 수 있습니다. 그러나 이것은 선택적 (채점하지 않는) 연습입니다. 우리는 또한 아래의 구현을 제공하므로 복사하거나 참조 할 수 있습니다. 예제를 복사하기로 결정했다면, Octave 문서를 참고하여 각각의 명령이 무엇을 하는지 배우십시오.
|
%
Find Indices of Positive and Negative Examples %
Plot Examples |
실 제 비용 함수로 시작하기 전에, 로지스틱 회귀 가설은 다음과 같이 정의됨을 기억하십시오 :
hθ(x) = g (θTx),
함 수 g는 시그 모이 드 함수입니다. 시그 모이 드 함수는 다음과 같이 정의됩니다.
g(z) = 1 / (1 + e-z).
첫 번째 단계는 sigmoid.m에서이 함수를 구현하여 나머지 프로그램에서 호출 할 수 있도록하는 것입니다. 끝나면 옥타브 명령 줄에서 sigmoid(x)를 호출하여 몇 가지 값을 테스트 해보십시오. x의 큰 양수 값의 경우 Sigmoid는 1에 가까워 야하지만 큰 음수 값의 경우 Sigmoid는 0에 가까워 야합니다. Sigmoid(0)을 평가하면 정확히 0.5가됩니다. 코드는 벡터와 행렬에서도 작동해야합니다. 행렬의 경우 함수는 모든 요소에서 시그 모이 드 함수를 수행해야합니다.
Octave 명령 줄에 submit을 입력하여 채점을위한 솔루션을 제출할 수 있습니다. 제출 스크립트는 사용자 이름과 암호를 묻는 메시지를 표시하고 제출할 파일을 묻습니다. 웹 사이트에서 제출 암호를 얻을 수 있습니다.
이 제 워밍업 연습을 제출해야 합니다.
이
제 로지스틱 회귀에 대한 비용 함수와 그
레디언트를 구현할 것입니다.
costFunction.m의 코드를 완성하여 비용과 그레디언트를 반환하십시오.
로지스틱 회귀 분석에서 비용 함수는 다음과 같다.
비 용의 기울기는 θ와 동일한 길이의 벡터이며, 여기서 j 번째 요소 (j = 0,1, ..., n의 경우)는 다음과 같이 정의됩니다.
이 그 레디언트는 선형 회귀 기울기와 동일하게 보이지만, 선형 및 회귀 회귀 분석에서는 hθ(x) 의 정의가 다르기 때문에 수식이 실제로는 다릅니다.
완 료되면 ex2.m은 θ의 초기 매개 변수를 사용하여 costFunction을 호출합니다. 비용은 약 0.693입니다.
이 제 물류 회귀에 대한 비용 함수와 그라디언트를 제출해야합니다. 두 가지 제출을 하십시오. 하나는 비용 함수이고 다른 하나는 그 레디언트 입니다.
이 전 과제에서는 계단 강하를 구현하여 선형 회귀 모델의 최적 매개 변수를 찾았습니다. 당신은 비용 함수를 작성하고 그 그라데이션을 계산 한 다음 그에 따라 그라데이션 디센트 단계를 취했습니다. 이번에는 그라디언트 디센트 단계를 사용하는 대신 fminunc라는 Octave 기본 제공 함수를 사용합니다.
Octave 의 fminunc는 unconstrained 함수의 최소값을 찾는 최적화 솔버입니다. 로지스틱 회귀 분석의 경우 매개 변수 θ를 사용하여 비용 함수 J (θ)를 최적화하려고합니다.
구 체적으로, fminunc를 사용하여 고정 된 데이터 집합 (X 및 Y 값)이 주어지면 로지스틱 회귀 비용 함수에 대해 최상의 매개 변수 θ를 찾습니다. 다음 입력을 fminunc로 전달합니다.
ex2.m 에서 fminunc를 올바른 인수로 호출하도록 작성된 코드가 이미 있습니다.
|
%
Set options for fminunc %
Run fminunc to obtain the optimal theta |
이 코드 스 니펫에서는 fminunc와 함께 사용할 옵션을 처음으로 정의했습니다. 구체적으로, GradObj 옵션을 on으로 설정하면 fminunc에 함수가 비용과 그라디언트를 반환합니다. 이렇게하면 함수를 최소화 할 때 fminunc가 그래디언트를 사용할 수 있습니다. 또한 MaxIter 옵션을 400으로 설정하여 fminunc가 종료되기 전에 400 단계까지 실행합니다.
우 리가 최소화하고있는 실제 함수를 지정하기 위해 @ (t) (costFunction (t, X, y))를 사용하여 함수를 지정하는 데 "짧은 손"을 사용합니다. 이렇게하면 costFunction을 호출하는 인수 t가있는 함수가 만들어집니다. 이렇게하면 fminunc와 함께 사용할 costFunction을 래핑 할 수 있습니다.
costFunction 을 올바르게 완료하면 fminunc는 올바른 최적화 매개 변수에 수렴하고 비용 및 θ의 최종 값을 반환합니다. fminunc를 사용하여 루프를 직접 작성하거나 그라디언트 디센트처럼 학습률을 설정할 필요가 없었습니다. 이것은 모두 fminunc에 의해 완료됩니다 : 당신은 비용과 그라디언트를 계산하는 함수를 제공 할 필요가있었습니다.
fminunc 가 완료되면 ex2.m은 θ의 최적 매개 변수를 사용하여 costFunction 함수를 호출합니다. 비용은 약 0.203입니다.
이 최종 θ 값은 트레이닝 데이터의 결정 경계를 그리는 데 사용되어 그림 2와 비슷한 결과를 얻습니다. 우리는 plotDecisionBoundary.m의 코드를보고이 경계를 그리는 방법을 살펴 보시기 바랍니다. θ 값.
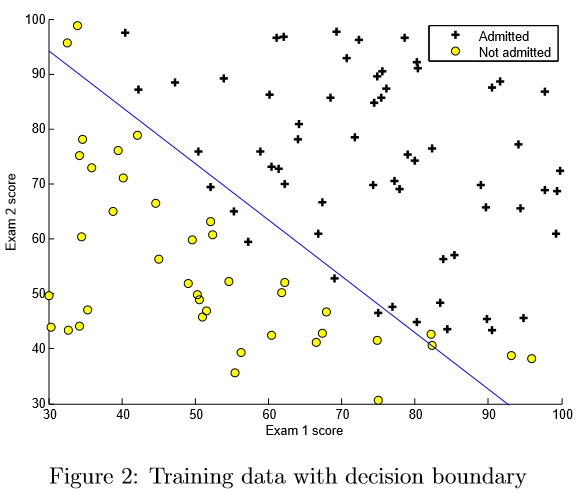
매 개 변수를 학습 한 후에 모델을 사용하여 특정 학생의 입학 여부를 예측할 수 있습니다. 시험 1 점이 45 점이고 시험 2 점이 85 점인 학생의 경우 입학 확률은 0.776입니다.
우 리가 발견 한 파라미터의 품질을 평가하는 또 다른 방법은 학습 된 모델이 우리의 교육 세트에서 얼마나 잘 예측되는지를 확인하는 것입니다. 이 파트에서는 predict.m의 코드를 완료하는 작업을 수행합니다. 예측 함수는 데이터 집합과 학습 된 매개 변수 벡터 θ에 대해 "1"또는 "0"예측을 생성합니다.
predict.m 에서 코드를 완료하면 ex2.m 스크립트는 올바른 예제의 비율을 계산하여 클래스의 교육 정확도를보고합니다.
이 제 로지스틱 회귀 예측 함수를 제출해야합니다.
이 연습에서는 가공 공장의 마이크로 칩이 품질 보증 (QA, Quality Assurance)을 통과 하는지를 예측하기 위해 규칙화된 로지스틱 회귀 분석을 구현합니다. 품질 보증 기간 동안 각 마이크로 칩은 올바르게 작동하는지 확인하기 위해 다양한 테스트를 거칩니다.
당 신이 공장의 제품 관리자이고 두 가지 다른 테스트에서 일부 마이크로 칩에 대한 테스트 결과가 있다고 가정 해보십시오. 이 두 가지 검사에서 마이크로 칩을 받아 들여야하는지 아니면 거절해야하는지 결정하고 싶습니다. 의사 결정을 돕기 위해 과거의 마이크로 칩에 대한 테스트 결과의 데이터 세트가 있습니다. 이로부터 로지스틱 회귀 모델을 구축 할 수 있습니다.
연 습의 이 부분을 완료하려면 ex2_reg.m이라는 다른 스크립트를 사용하십시오.
이 연습의 이전 부분과 마찬가지로 plotData를 사용하여 그림 3과 같은 그림을 생성합니다. 여기서 축은 두 개의 테스트 점수이고 양수 (y = 1, 허용) 및 음수 (y = 0, 거부) 예제는 다른 마커와 함께 표시됩니다.
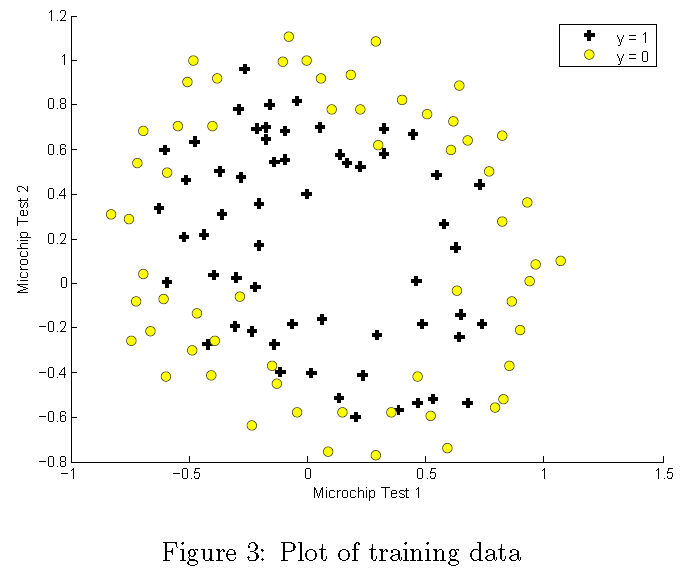
그 림 3은 우리의 데이터 세트가 플롯을 통해 직선으로 양수 및 음수 예제로 분리 될 수 없음을 보여줍니다. 따라서 로지스틱 회귀의 직관적인 적용은 로지스틱 회귀가 선형 결정 경계 만 찾을 수 있기 때문에 이 데이터 세트에서 잘 수행되지 않습니다.
데 이터를 더 잘 맞추는 한 가지 방법은 각 데이터 요소에서 더 많은 특징을 만드는 것입니다. 제공된 함수 mapFeature.m에서 우리는 x1과 x2의 모든 다항식 항으로 특징를 6 차까지 매핑합니다.
이 매핑의 결과로 두 개의 피쳐 (두 개의 QA 테스트의 점수) 벡터가 28 차원 벡터로 변형되었습니다. 이 더 높은 차원의 특성 벡터에 대해 학습 된 로지스틱 회귀 분류자는보다 복잡한 결정 경계를 가지며 2 차원 플롯에서 그릴 때 비선형으로 나타납니다.
특 징 매핑을 사용하면 보다 표현력있는 분류 기준을 만들 수 있지만 지나치게 적합(적응)되기 쉽습니다. 연습의 다음 부분에서는 데이터에 맞게 정규화 된 로지스틱 회귀를 구현하고 정규화가 어떻게 과적합 문제를 해결하는 데 도움이되는지 직접 확인하게 됩니다.
이 제 정규화 된 로지스틱 회귀에 대한 비용 함수 및 그래디언트를 계산하는 코드를 구현합니다. costFunctionReg.m의 코드를 완료하여 비용 및 그래디언트를 반환하십시오.
로 지스틱 회귀에서의 정규화 된 비용 함수는 다음과 같다.
매 개 변수 θ0를 정규화해서는 안됩니다. 옥타브에서는 인덱싱이 1부터 시작하므로 코드에서 theta(1) 파아메타 ( θ0 에 해당)를 정규화해서는 안됩니다. 비용 함수의 기울기는 j 번째 요소가 다음과 같이 정의되는 벡터입니다.
완 료되면 ex2 reg.m은 (모두 0으로 초기화 된) 초기 값을 사용하여 costFunctionReg 함수를 호출합니다. 비용은 약 0.693입니다.
이 제 정규화 된 물류 회귀에 대한 비용 함수와 그라디언트를 제출해야합니다. 비용 함수와 그라디언트에 대해 하나씩 제출하십시오.
이 전 부분과 마찬가지로 fminunc를 사용하여 최적의 매개 변수를 학습합니다. 정규화 된 로지스틱 회귀 (costFunctionReg.m)에 대한 비용 및 그래디언트를 올바르게 완료 한 경우 fminunc를 사용하여 매개 변수를 배우려면 ex2 reg.m의 다음 단계를 수행 할 수 있어야 합니다.
이 분류 기준에서 학습 한 모델을 시각화하는 데 도움이되도록 plotDecisionBoundary.m 함수에 양수 및 음수 예제를 구분하는 (비선형) 결정 경계를 표시합니다. plotDecisionBoundary.m에서 균등하게 간격을 둔 그리드에서 분류 기준의 예측을 계산하여 비선형 결정 경계를 플롯 한 다음 예측이 y = 0에서 y = 1로 변경되는 윤곽 플롯을 그립니다.
매 개 변수를 학습 한 후 ex reg.m의 다음 단계는 그림 4와 유사한 결정 경계를 그릴 것입니다.
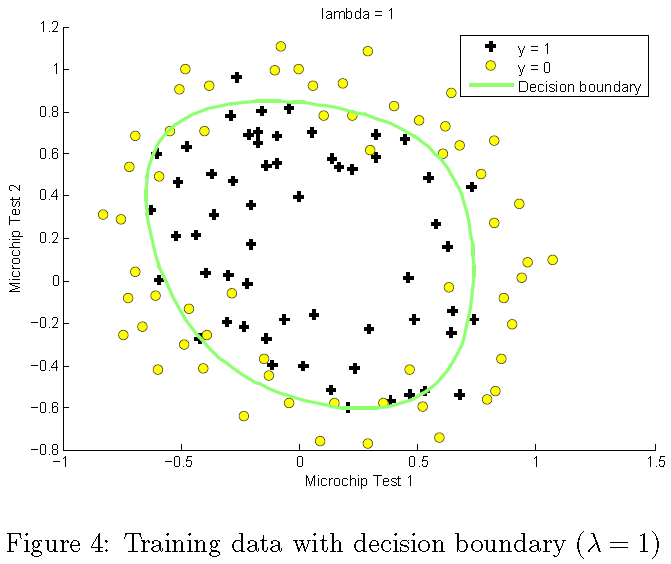
이 번 연습에서는 정규화가 어떻게 과적합을 방지 하는 지를 이해하기 위해 데이터 집합에 대해 다른 정규화 매개 변수를 시험해 볼 것입니다.
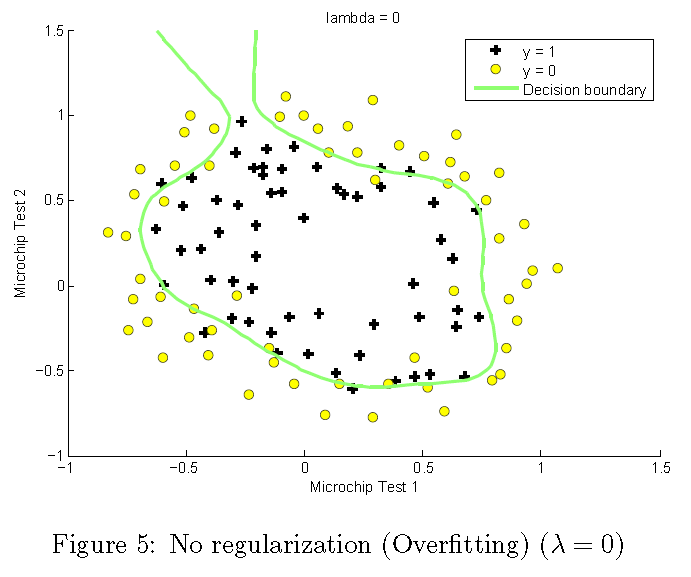
λ 변화에 따라 결정 경계의 변화를 확인하십시오. 작은 λ 의 경우 분류기가 거의 모든 훈련 예제를 올바로 분류할 수 있지만, 매우 복잡한 경계를 그려서 데이터에 초과 적용됩니다 (그림 5). 이것은 좋은 결정 경계가 아닙니다. 예를 들어, x = (-0.25, 1.5)에있는 점이 허용되며 (y = 1), 이는 훈련 자료 세트에서 잘못된 결정으로 보입니다.
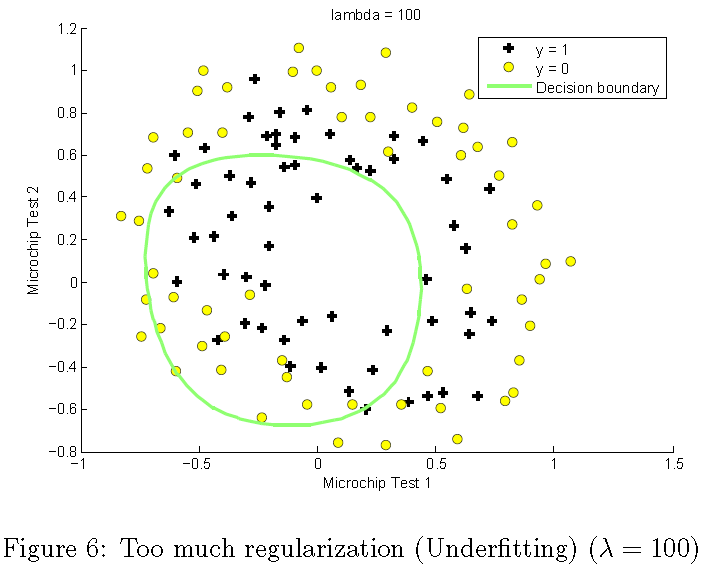
더 큰 λ 값을 사용하면 긍정적인 결과와 네거티브를 상당히 잘
구분하는 간단한 결정 경계를 나타내는 플롯을 보아야 합니다. 그러나 λ 값을 너무 크게 설정하면 잘 맞지 않으며 의사 결정
경계가 데이터를 잘 따르지 않아 데이터에 미적합되게 됩니다 (그림 6).
이 러한 추가 연습에 대한 답을 제출할 필요는 없습니다.
다 음은 이 연습의 각 부분이 채점되는 방식에 대한 분석입니다.
| Part | Submitted File | Points |
| Sigmoid Function | sigmoid.m | 5 points |
|
Compute
cost for logistic regression |
costFunction.m |
30
points |
| Compute
cost for regularized LR Gradient for regularized LR |
costFunctionReg.m costFunctionReg.m |
15
points 15 points |
| Total Points | 100 points |